L'impossible mesure de Pi
+2
Bean
Jean Ghislain
6 participants
Page 1 sur 1
 L'impossible mesure de Pi
L'impossible mesure de Pi
Aucune régularité ou périodicité n'a jamais été constatée dans les décimales de Pi . Pourtant, on part bien du réel, puisque de fait, le nombre Pi est défini par un certain rapport entre le cercle et son rayon, donc un rapport bel et bien donné ! Cependant, ce rapport n'est pas mesurable exactement. En géométrie, de façon pratique, j'ai une règle pour mesurer un rayon. Mettons cette règle mesure 1. A-t-on une méthode qui utilise cette règle pour mesurer la circonférence et donc tomber sur Pi ?
Sachant que la règle étant droite, tandis la circonférence est courbe, on ne peut que faire des approximations, avec des mesures répétés à partir de la règle qui donne la mesure. Or qui dit approximations, dit forcément erreur de mesure. Qui dit erreur de mesure répété dit aussi que même si l'on va à l'infini de n'importe quelle méthode avancé, l'infini ne pourra jamais rattraper le fait que l'erreur se retrouve, même si l'erreur devient infiniment petite, l'erreur étant déjà là, et son existence se répète même si allant s'amoindrissant.
Cela signifie que Pi est assez hasardeux à trouver, géométriquement comme je l'ai illustré, mais aussi mathématiquement à caractériser si l'on veut l'exprimer rationnellement, quand bien même on répète à l'infini n'importe quel procédé, le hasard semblant avoir sa place dans la construction du nombre Pi.
Partant de la réalité et des rapports entre les objets de la réalité, existe-t-il une méthode pour arriver à une formule qui décrirait exactement ce rapport ?
Ouvrons une piste moderne.
Le rapport du cercle au diamètre est Pi.
Si l'on observe ce rapport, directement ou par des descriptions déjà faite, on en vient à vouloir formuler ce rapport. Géométriquement parlant, et de fait, le rapport ne peut être obtenu par la mesure.
En faisant intervenir la physique, qui engage le temps, cela offre aussi une ouverture. En physique, la réalité du mouvement (des objets), se fait par puissance, c'est-à-dire par l'application dans le temps d'une force répété sur l'objet. La puissance étant l'application de la force dans le temps.
Un petit détour par les maths me fait dire :
Pi = -i.ln(-1), soit sous sa forme d'Euler
e^(i.Pi) = - 1 (notons que les hippies n'ont rien à voir là-dedans)
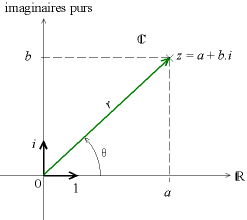
soit dans ce plan complexe ci-dessus, on a la correspondance entre e^(i.teta) = z, le point correspondant à Pi n'étant qu'un point où teta congru à Pi + 2n.Pi, et qui donne z = -1. On a la correspondance entre 1 et Pi !
Petit questionnement métaphysique, en revenant sur le terrain de la physique, en notant teta = t (variable de temps). On voit alors que selon le temps croissant, le mobile positionné en z, parcours de fait le cercle.
Or qu'est-ce qui fait parcourir le mobile sur le cercle ? Où est la force qui s'applique, qui conjugué au temps donne la puissance nécessaire pour mouvoir le mobile, c-à-d le faire changer de place ? Mystère...(la gravitation ?) De là on peut très bien décrire les caractéristiques d'une force, et sa puissance, mais quelle en est l'origine, quand elle est là, dans le cas où l'on voit un mouvement ?
En fait c'est un peu trouver le fonctionnement moteur d'un mouvement. Si une chose continue à se mouvoir, nous apprend un principe de physique, c'est par conservation d'une énergie. Mais d'où vient cette énergie ? L'énergie se conservant, si le mobile perd de la vitesse, l'énergie perdue se disperse. Si l'on prend maintenant l'ensemble du système énergétique, on voit que tout devient de plus en plus désordonné. Mais est-ce à dire qu'il y a eu un ordre premier dans le temps, à l'origine ? D'où viendrait alors cette énergie première ?
Autant de questions, et aucune réponse première, puisqu'à chaque fois, le même problème revient : Si la science comprend le comment des choses-là, elle n'explique pas le pourquoi de cette présence.
Sachant que la règle étant droite, tandis la circonférence est courbe, on ne peut que faire des approximations, avec des mesures répétés à partir de la règle qui donne la mesure. Or qui dit approximations, dit forcément erreur de mesure. Qui dit erreur de mesure répété dit aussi que même si l'on va à l'infini de n'importe quelle méthode avancé, l'infini ne pourra jamais rattraper le fait que l'erreur se retrouve, même si l'erreur devient infiniment petite, l'erreur étant déjà là, et son existence se répète même si allant s'amoindrissant.
Cela signifie que Pi est assez hasardeux à trouver, géométriquement comme je l'ai illustré, mais aussi mathématiquement à caractériser si l'on veut l'exprimer rationnellement, quand bien même on répète à l'infini n'importe quel procédé, le hasard semblant avoir sa place dans la construction du nombre Pi.
Partant de la réalité et des rapports entre les objets de la réalité, existe-t-il une méthode pour arriver à une formule qui décrirait exactement ce rapport ?
Ouvrons une piste moderne.
Le rapport du cercle au diamètre est Pi.
Si l'on observe ce rapport, directement ou par des descriptions déjà faite, on en vient à vouloir formuler ce rapport. Géométriquement parlant, et de fait, le rapport ne peut être obtenu par la mesure.
En faisant intervenir la physique, qui engage le temps, cela offre aussi une ouverture. En physique, la réalité du mouvement (des objets), se fait par puissance, c'est-à-dire par l'application dans le temps d'une force répété sur l'objet. La puissance étant l'application de la force dans le temps.
Un petit détour par les maths me fait dire :
Pi = -i.ln(-1), soit sous sa forme d'Euler
e^(i.Pi) = - 1 (notons que les hippies n'ont rien à voir là-dedans)

soit dans ce plan complexe ci-dessus, on a la correspondance entre e^(i.teta) = z, le point correspondant à Pi n'étant qu'un point où teta congru à Pi + 2n.Pi, et qui donne z = -1. On a la correspondance entre 1 et Pi !
Petit questionnement métaphysique, en revenant sur le terrain de la physique, en notant teta = t (variable de temps). On voit alors que selon le temps croissant, le mobile positionné en z, parcours de fait le cercle.
Or qu'est-ce qui fait parcourir le mobile sur le cercle ? Où est la force qui s'applique, qui conjugué au temps donne la puissance nécessaire pour mouvoir le mobile, c-à-d le faire changer de place ? Mystère...(la gravitation ?) De là on peut très bien décrire les caractéristiques d'une force, et sa puissance, mais quelle en est l'origine, quand elle est là, dans le cas où l'on voit un mouvement ?
En fait c'est un peu trouver le fonctionnement moteur d'un mouvement. Si une chose continue à se mouvoir, nous apprend un principe de physique, c'est par conservation d'une énergie. Mais d'où vient cette énergie ? L'énergie se conservant, si le mobile perd de la vitesse, l'énergie perdue se disperse. Si l'on prend maintenant l'ensemble du système énergétique, on voit que tout devient de plus en plus désordonné. Mais est-ce à dire qu'il y a eu un ordre premier dans le temps, à l'origine ? D'où viendrait alors cette énergie première ?
Autant de questions, et aucune réponse première, puisqu'à chaque fois, le même problème revient : Si la science comprend le comment des choses-là, elle n'explique pas le pourquoi de cette présence.

Jean Ghislain- Sorti de l'oeuf
-
 Nombre de messages : 23
Nombre de messages : 23
Localisation : Auvergne-Rhône-Alpes.
Identité métaphysique : philosophe
Humeur : et la tienne ?
Date d'inscription : 21/02/2015
 Re: L'impossible mesure de Pi
Re: L'impossible mesure de Pi
ei.Pi = -1 formule qui renferme un entier relatif, deux nombres transcendants et un nombre imaginaire.
Comment réaliser une proportion avec une telle formule!
C = Pi.D permet de mieux cerner la proportion de Pi qui est Pi = C / D donc un rapport de deux longueurs, circonférence et diamètre d'un cercle.
Et donc pour D = 1 ; C = Pi
Un développement en fractions de Pi est possible:
pi(n) = 2 + (2/(1+1/(1/2)+1/(1/3)+1/(1/4)+1/....+1/(1/n)))))))
Plus n sera grand et plus le nombre fractionnaire obtenu sera proche de Pi et à la limite si n tend vers l'infini, pi(n) tend vers Pi
Pi est comme Achille voulant rattraper la tortue, il s'en approche mais ne l'atteint jamais.
Comment réaliser une proportion avec une telle formule!
C = Pi.D permet de mieux cerner la proportion de Pi qui est Pi = C / D donc un rapport de deux longueurs, circonférence et diamètre d'un cercle.
Et donc pour D = 1 ; C = Pi
Un développement en fractions de Pi est possible:
pi(n) = 2 + (2/(1+1/(1/2)+1/(1/3)+1/(1/4)+1/....+1/(1/n)))))))
Plus n sera grand et plus le nombre fractionnaire obtenu sera proche de Pi et à la limite si n tend vers l'infini, pi(n) tend vers Pi
Pi est comme Achille voulant rattraper la tortue, il s'en approche mais ne l'atteint jamais.

Bean- Seigneur de la Métaphysique
-
 Nombre de messages : 6964
Nombre de messages : 6964
Localisation : Bretagne
Identité métaphysique : Farceur
Humeur : Joyeux
Date d'inscription : 16/04/2012
 Re: L'impossible mesure de Pi
Re: L'impossible mesure de Pi
En 1994, David Chudnovsky et les frères Gregory proposent une formule fournissant 14 décimales à chaque itération :
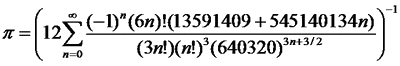
10 000 milliards de décimales de Pi sont connues aujourd'hui.
Ce sont deux informaticiens (un japonais et un américain), Alexander J. Yee & Shigeru Kondo, qui détiennent le record depuis le 17 octobre 2011.
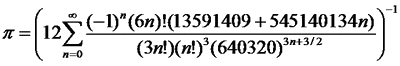
10 000 milliards de décimales de Pi sont connues aujourd'hui.
Ce sont deux informaticiens (un japonais et un américain), Alexander J. Yee & Shigeru Kondo, qui détiennent le record depuis le 17 octobre 2011.

Jean Ghislain- Sorti de l'oeuf
-
 Nombre de messages : 23
Nombre de messages : 23
Localisation : Auvergne-Rhône-Alpes.
Identité métaphysique : philosophe
Humeur : et la tienne ?
Date d'inscription : 21/02/2015
 Re: L'impossible mesure de Pi
Re: L'impossible mesure de Pi
Pour atteindre une précision de l'ordre de la longueur de Planck, la précision du nombre Pi pour un cercle de 1m de diamètre devrait être de l'ordre de 10-35 soit 100 millions de milliards de milliards de milliards de décimales.
Rapporté à la taille de l'univers observable (90 milliards d'années lumière = 1027 mètres) , la précision devrait être de 10-62 soit 100 millions de milliards de milliards de milliards de milliards de milliards de milliards de décimales.
On aurait alors une précision théorique ultime puisque rien ne peut être mesuré au delà de l'univers observable ni en deçà de la longueur de Planck.
Rapporté à la taille de l'univers observable (90 milliards d'années lumière = 1027 mètres) , la précision devrait être de 10-62 soit 100 millions de milliards de milliards de milliards de milliards de milliards de milliards de décimales.

On aurait alors une précision théorique ultime puisque rien ne peut être mesuré au delà de l'univers observable ni en deçà de la longueur de Planck.

Bean- Seigneur de la Métaphysique
-
 Nombre de messages : 6964
Nombre de messages : 6964
Localisation : Bretagne
Identité métaphysique : Farceur
Humeur : Joyeux
Date d'inscription : 16/04/2012
 Re: L'impossible mesure de Pi
Re: L'impossible mesure de Pi
Salut JG, j'ai l'impression qu'on va bien s'amuser nous deux! 
Quand à l'impossibilité d'atteindre une précision parfaite, ne serait-ce pas la source du hasard?

D'où vient l'inertie? Mais [Vous devez être inscrit et connecté pour voir ce lien] voyons!JG a écrit:En fait c'est un peu trouver le fonctionnement moteur d'un mouvement. Si une chose continue à se mouvoir, nous apprend un principe de physique, c'est par conservation d'une énergie. Mais d'où vient cette énergie ?
Quand à l'impossibilité d'atteindre une précision parfaite, ne serait-ce pas la source du hasard?

M'enfin- Le Repteux
-
 Nombre de messages : 10570
Nombre de messages : 10570
Localisation : Val David, Québec
Identité métaphysique : M'enfin...
Humeur : ...qui sait?
Date d'inscription : 24/02/2013
 Re: L'impossible mesure de Pi
Re: L'impossible mesure de Pi
Jean Ghislain a écrit:En 1994, David Chudnovsky et les frères Gregory proposent une formule fournissant 14 décimales à chaque itération :
10 000 milliards de décimales de Pi sont connues aujourd'hui.
Ce sont deux informaticiens (un japonais et un américain), Alexander J. Yee & Shigeru Kondo, qui détiennent le record depuis le 17 octobre 2011.
J'aime pas trop la formule d'Euler, je préfère la formule de fagnano, elle ne fait pas intervenir d'addition directement.

Critias- Affranchi des Paradoxes
-
 Nombre de messages : 227
Nombre de messages : 227
Localisation : Sud est
Identité métaphysique : Pataphysicien
Humeur : Sérieux
Date d'inscription : 25/12/2014
 Re: L'impossible mesure de Pi
Re: L'impossible mesure de Pi
Bonjour Jean-Ghislain.
Je ne comprends rien à votre message (ça mets tout de suite un cadre !).
Qu'entendez-vous par mesure d'un nombre ? Car vous parlez de mesurer Pi.
Toute mesure au sens physique est dotée d'une incertitude (enfin je crois) ; mais concernant le nombre Pi, il est défini exactement. Sans aucune incertitude. On sait qu'il est transcendant. Donc qu'on ne peut pas l'écrire complètement sous forme décimale. Mais il est parfaitement défini.
Cdt
Je ne comprends rien à votre message (ça mets tout de suite un cadre !).
Qu'entendez-vous par mesure d'un nombre ? Car vous parlez de mesurer Pi.
Toute mesure au sens physique est dotée d'une incertitude (enfin je crois) ; mais concernant le nombre Pi, il est défini exactement. Sans aucune incertitude. On sait qu'il est transcendant. Donc qu'on ne peut pas l'écrire complètement sous forme décimale. Mais il est parfaitement défini.
Cdt
Spontz- Sorti de l'oeuf
-
 Nombre de messages : 32
Nombre de messages : 32
Localisation : à l'ouest
Identité métaphysique : Généralement rationnel
Humeur : = mauvaise Si loin(apéro)
Date d'inscription : 20/09/2016
 Re: L'impossible mesure de Pi
Re: L'impossible mesure de Pi
Bonjour Spontz,
je te demanderais de ne pas changer les titres des fils stp, merci.
je te demanderais de ne pas changer les titres des fils stp, merci.
_________________
- Méfie-toi du boeuf par devant, de la mule par derrière et du moine de tous les côtés.
Cervantes
 Sujets similaires
Sujets similaires» La mesure poétique.
» Sagesse du pluvian
» Mesure de prévention contre l'alcoolisme
» Le droit de manifester et la répression sans mesure
» Serait-on en mesure d'élire un gouvernement intelligent ?
» Sagesse du pluvian
» Mesure de prévention contre l'alcoolisme
» Le droit de manifester et la répression sans mesure
» Serait-on en mesure d'élire un gouvernement intelligent ?
Page 1 sur 1
Permission de ce forum:
Vous ne pouvez pas répondre aux sujets dans ce forum